一、平方差公式(formula for the difference of squares)

(a+b)(a-b)=a²-b²

    两个数的和与这两个数的差的积，等于这两个数的平方差。

二、完全平方公式(formula for the square of the sum)

(a+b)²=a²+2ab+b²

(a-b)²=a²-2ab+b²

    两个数的和(或差)的平方，等于它们的平方和，加上(或减去)它们的积的2倍。

三、练习题

1、用整式的乘法推导平方差公式和完全平方公式。

2、用公式计算：

（1）(a+b+c)(a+b-c)

（2）(a-b+c)²

3、已知a+b=8，ab=14，求a²+b²的值。

四、杨辉三角    

    我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中用上图的三角形解释二项和的乘方规律。因为杨辉在注释中提到，在他之前北宋数学家贾宪(1050年左右)也用过上述方法，因此我们称这个三角形为“杨辉三角”或“贾宪三角”。

    法国数学家帕斯卡( Pascal,1623-1662)于1654年发现了此三角形，这个三角形被欧洲学者称为“帕斯卡三角”。

    杨辉三角两腰上的数都是1，其余每个数为它的上方（左右）两数之和。事实上，这个三角形给出了

的展开式（按a的次数由大到小的顺序）的系数规律。例如，此三角形中第3行的3个数1，2，1，恰好对应着(a+b)²=a²+2ab+b²展开式中的各项的系数；第4行的4个数1，3，3，1，恰好对应着(a+b)³=a³+3a²b+3ab²+b³展开式中各项的系数，等等。

五、Python学习时间

    用Python和杨辉三角推算展开

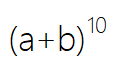
后各项的系数。

Python代码：

#杨辉三角

#最后次数

maxNum=10

#推算列表

lst=[1,1]

#打印杨辉三角

print("00：1")

print("01：", end="")      #end=""不换行

print(lst[0], end="\t")    #end="\t"以制表符结束

print(lst[1])

for n in range(2, maxNum+1):

    #打印行号，就是次数

    if(n<10):

        print("0"+str(n)+"：", end="")     

    else:

        print(str(n)+"：", end="")

    #打印首项

    print(lst[0], end="\t")          

    #列表往前推进一次

    temp0=lst[0]            #上一行左项

    for m in range(1, n):

        temp1=lst[m]        #上一行右项

        lst[m]+=temp0       #当前行项

        temp0=temp1         #把上一行右项赋值给上一行左项准备下一轮循环

        print(lst[m], end="\t")  #打印该项

    lst.append(1)                #添加最后一项

    print(lst[n])                #打印最后一项

输出结果：

练习：改编程序，推算展开

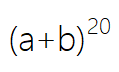
后各项的系数，并只打印出结果行。

​