角度和弧度是量角的两种单位,但它们有以下差别:
1、角度是一种方向,弧度是线的长短比例;
2、人类对角度比较有直觉,对弧度缺乏直觉,所以角度多用于输入输出;
3、由于弧度是线的长短比例,所以与角或旋转有关的内核运算一律使用弧度,为了减少公式的记忆量,只需记忆用弧度的公式及转换公式。
由上一课中,我们得知,当圆内接正对多边形的边数趋向无穷大时,实际就和圆无可区别,即圆是圆内接正多边形的极限,这时周长C和半径R有下面的关系:
C/(2R)=π。
等式两边同时乘2R得圆的周长计算公式:
C=2πR。
根据弧度制的规定,弧长是半径的弧所对的圆心角为1弧度,得一个周角的弧度数值是:
C÷R=2πR÷R=2π。
根据角度制的规定,一个周角是360°,所以角度和弧度的单位换算公式是:
1°=2π/360=π/180(弧度)。
α弧度的圆心角所对的弧长为(弧长计算公式):
l=2πR×(α/2π)=αR。
即弧长等于弧度乘半径。当α=2π(即周角)时,是圆的周长计算公式。
由于
n°=nπ/180(弧度),
所以n°的圆心角所对的弧长为:
l=nπR/180。
有关圆的计算公式不少,但它们的根公式是弧长计算公式、角度和弧度的单位换算公式。
也可以用
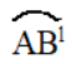
表示
![]()
的长。
例1 制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,计算下图所示的管道的展直长度L(结果取整数)。

解:由弧长公式,得弧AB的长
l=100×900×π÷180=500π≈1570(mm)。
因此所要求的展直长度
L=2×700+1570=2970(mm)。
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。可以发现,扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关,圆心角越大,扇形面积也就越大,在半径一定时,面积与圆心角成正比例关系。

在半径为R的圆中,因为2π(弧度)的圆心角所对的扇形的面积就是圆面积
S=πR²,
所以圆心角是α(弧度)的扇形面积是
S=πR²×(α/2π)=½αR²=½(αR)×R=½lR。
即扇形的面积等于弧长乘半径的一半。与三角形的面积公式一样,只不过是底边变成弧长,高变为半径,结合圆的面积推导过程,这个容易理解。
于是,把n°=nπ/180(弧度)代入上面公式中的α,得圆心角为n°的扇形面积是
S=½(nπ/180)R²=nπR²/360。
例2 如下图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m。求截面上有水部分的面积(结果保留小数点后两位)。

解:如下图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C。
∵ OC=0.6m,DC=0.3m,
∴ OD=OC-DC=0.3(m)。
又 AD⊥OD,
∴ ∠OAD=30°,AD=√3OD,(直角边是斜边一半的对角是30°)
∴ ∠AOB=(90°-30°)×2=120°,AB=2AD=0.6√3。
有水部分的面积
S=S扇形OAB-S△OAB
=120π/360×0.6²-½AB·OD
=0.12π-½×0.6√3x0.3
≈0.22(m²)。

练习题1
1. 弧长相等的两段弧是等弧吗?
2. 如下图,有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81°。这段圆弧所在圆的半径R是多少米(结果保留小数点后一位)?

3. 如下图,正三角形ABC的边长为a,D,E,F分别为BC,CA,AB的中点,以A,B,C三点为圆心,½a长为半径作圆。求图中阴影部分的面积。

我们知道,圆锥是由一个底面和一个侧面围成的几何体,如下图,我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。

把圆锥侧放,然后底圆一点转一圈,会是什么图形?即圆锥的侧面展开图是什么图形?
如下图,圆锥的侧面展开图是一个扇形。设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl,圆锥的全面积为πr(r+l)。

例3 如下图,蒙古包可以近似地看作由圆锥和圆柱组成。如果想用毛毡搭建20个底面积为12m²,高为3.2m,外围高1.8m的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)?

解:下图是一个蒙古包的示意图。根据题意,下部圆柱的底面积为12m²,高h2=1.8m;上部圆锥的高h1=3.2-1.8=1.4(m)。
圆柱的底面圆的半径
r=√(12/π)≈1.954(m),
侧面积为
2π×1.954×1.8≈22.10(m²)。
圆锥的母线长
l=√(1.954²+1.4²)≈2.404(m),
侧面展开扇形的弧长为
2π×1.954≈12.28(m),
圆锥的侧面积为
½×2.404X12.28≈14.76(m²)。
因此,搭建20个这样的蒙古包至少需要毛毡
20×(22.10+14.76)≈738(m²)。

练习题2
1. 圆锥的底面直径是80cm,母线长90cm。求它的侧面展开图的圆心角和圆锥的全面积。
2. 如下图,圆维形的烟囱帽的底面圆的直径是80cm,母线长是50cm,制作100个这样的烟囱帽至少需要多少平方米的铁皮?


