有关浮点数 通过提升精度来解决精确数舍入错误。
使用十进制精确数可以消除浮点数的表示错误（即能够完全精确地表示 0.1 这样的数）；然而，某些运算在非零数位超出给定的精度时仍然可能导致舍入错误。 舍入错误的影响可能因加减几乎可以忽略不计的数而被放大，从而导致有效数位丢失。Knuth 提供了两个非常有用的例子，由于精度不足而产生的浮点舍入影响，导致加法的交换律和分配律被打破：
# Examples from Seminumerical Algorithms, Section 4.2.2.
>>> from decimal import Decimal, getcontext
>>> getcontext().prec = 8
>>> u, v, w = Decimal(11111113), Decimal(-11111111), Decimal('7.51111111')
>>> (u + v) + w
Decimal('9.5111111')
>>> u + (v + w)
Decimal('10')
>>> u, v, w = Decimal(20000), Decimal(-6), Decimal('6.0000003')
>>> (u*v) + (u*w)
Decimal('0.01')
>>> u * (v+w)
Decimal('0.0060000')
decimal 模块则可以通过提高足够的精度来避免有效位的丢失：
getcontext().prec = 20
>>> u, v, w = Decimal(11111113), Decimal(-11111111), Decimal('7.51111111')
>>> (u + v) + w
Decimal('9.51111111')
>>> u + (v + w)
Decimal('9.51111111')
>>>
>>> u, v, w = Decimal(20000), Decimal(-6), Decimal('6.0000003')
>>> (u*v) + (u*w)
Decimal('0.0060000')
>>> u * (v+w)
Decimal('0.0060000')
几个特殊的值
decimal模块的数字系统提供了一些特殊的值，包括NaN，sNaN，-Infinity，Infinity， 以及两种零值 +0 和 -0。 Infinity（无穷大）可以使用 Decimal('Infinity') 来直接构造。
它们也可以在不捕获 DivisionByZero 信号时通过除以零来产生。
类似地，当不捕获 Overflow 信号时，也可以通过舍入到超出最大可表示数字限制的方式产生无穷大的结果。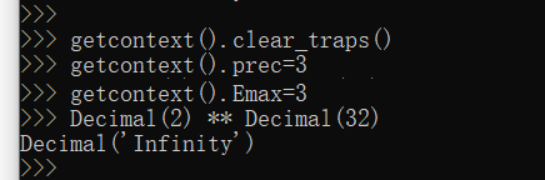
无穷大是有符号的（仿射的）并可用于算术运算，它们会被当作极其巨大的不确定数字来处理。例如，无穷大加一个常量结果也将为无穷大。
某些不存在有效结果的运算将会返回NaN，或者，如果设置捕获InvalidOperation信号则会引发一个异常。例如，0/0 会返回 NaN 表示结果“不是一个数字”。这样的 NaN 是静默产生的，并且在产生之后参与其它计算时总是会得到 NaN 的结果。这种行为对于偶而缺少输入的各类计算都很有用处 --- 它允许在将特定结果标记为无效的同时让计算继续运行。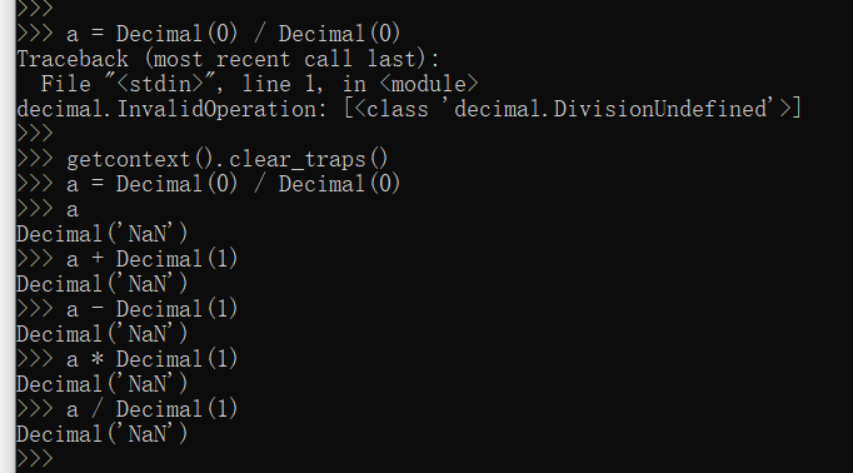
另一种变化形式是sNaN（显式），它在每次运算后会发出信号而不是保持静默。当对于无效结果需要中断计算进行特别处理时，这是一个很有用的返回值。
Python 中比较运算符的行为在涉及 NaN 时可能会令人有点惊讶。相等性检测在操作数中有静默型或信号型 NaN 时总是会返回 False (即使是执行 Decimal('NaN')==Decimal('NaN'))，而不等性检测总是会返回 True。
当尝试使用 <, <=, > 或 >= 运算符中的任何一个来比较两个 Decimal 值时，如果运算数中有 NaN 则将引发 InvalidOperation 信号，如果此信号未被捕获则将返回 False。
请注意通用精确数算术规范并未规定直接比较行为；这些涉及 NaN 的比较规则来自于 IEEE 854 标准。要确保严格符合标准，请改用 compare() 和 compare-signal() 方法。
有符号零值可以由向下溢出的运算产生。它们保留符号是为了让运算结果能以更高的精度传递。由于它们的大小为零，正零和负零会被视为相等，且它们的符号具有信息。
除了这两个不相同但却相等的有符号零之外，还存在几种零的不同表示形式，它们的精度不同但值也都相等。这需要一些时间来逐渐适应。对于习惯了标准浮点表示形式的人来说，以下运算返回的值等于零，不是显而易见的：
使用线程
getcontext() 函数会为每个线程访问不同的 Context 对象。具有单独线程上下文意味着线程可以修改上下文 (例如 getcontext().prec=10) 而不影响其他线程。
类似的 setcontext() 只会赋值给当前线程的上下文。
如果在调用setcontext()之前调用 getcontext()，则 getcontext() 将创建一个新的上下文用于当前线程。
新的上下文拷贝自一个名为 DefaultContext 的原型上下文。要控制默认值以便每个线程在应用运行期间都使用相同的值，可以直接修改 DefaultContext 对象。这应当在任何线程启动之前完成，以使得调用 getcontext() 的线程之间不会产生条件冲突。例如:
# Set applicationwide defaults for all threads about to be launched
DefaultContext.prec = 12
DefaultContext.rounding = ROUND_DOWN
DefaultContext.traps = ExtendedContext.traps.copy()
DefaultContext.traps[InvalidOperation] = 1
setcontext(DefaultContext)
# Afterwards, the threads can be started
t1.start()
t2.start()
t3.start()
. . .
例程 以下是一些用作工具函数的例程，它们演示了使用 Decimal 类的各种方式:
def moneyfmt(value, places=2, curr='', sep=',', dp='.',
pos='', neg='-', trailneg=''):
"""Convert Decimal to a money formatted string.
places: required number of places after the decimal point
curr: optional currency symbol before the sign (may be blank)
sep: optional grouping separator (comma, period, space, or blank)
dp: decimal point indicator (comma or period)
only specify as blank when places is zero
pos: optional sign for positive numbers: '+', space or blank
neg: optional sign for negative numbers: '-', '(', space or blank
trailneg:optional trailing minus indicator: '-', ')', space or blank
>>> d = Decimal('-1234567.8901')
>>> moneyfmt(d, curr='$')
'-$1,234,567.89'
>>> moneyfmt(d, places=0, sep='.', dp='', neg='', trailneg='-')
'1.234.568-'
>>> moneyfmt(d, curr='$', neg='(', trailneg=')')
'($1,234,567.89)'
>>> moneyfmt(Decimal(123456789), sep=' ')
'123 456 789.00'
>>> moneyfmt(Decimal('-0.02'), neg='<', trailneg='>')
'<0.02>'
"""
q = Decimal(10) ** -places # 2 places --> '0.01'
sign, digits, exp = value.quantize(q).as_tuple()
result = []
digits = list(map(str, digits))
build, next = result.append, digits.pop
if sign:
build(trailneg)
for i in range(places):
build(next() if digits else '0')
if places:
build(dp)
if not digits:
build('0')
i = 0
while digits:
build(next())
i += 1
if i == 3 and digits:
i = 0
build(sep)
build(curr)
build(neg if sign else pos)
return ''.join(reversed(result))
def pi():
"""Compute Pi to the current precision.
>>> print(pi())
3.141592653589793238462643383
"""
getcontext().prec += 2 # extra digits for intermediate steps
three = Decimal(3) # substitute "three=3.0" for regular floats
lasts, t, s, n, na, d, da = 0, three, 3, 1, 0, 0, 24
while s != lasts:
lasts = s
n, na = n+na, na+8
d, da = d+da, da+32
t = (t * n) / d
s += t
getcontext().prec -= 2
return +s # unary plus applies the new precision
def exp(x):
"""Return e raised to the power of x. Result type matches input type.
>>> print(exp(Decimal(1)))
2.718281828459045235360287471
>>> print(exp(Decimal(2)))
7.389056098930650227230427461
>>> print(exp(2.0))
7.38905609893
>>> print(exp(2+0j))
(7.38905609893+0j)
"""
getcontext().prec += 2
i, lasts, s, fact, num = 0, 0, 1, 1, 1
while s != lasts:
lasts = s
i += 1
fact *= i
num *= x
s += num / fact
getcontext().prec -= 2
return +s
def cos(x):
"""Return the cosine of x as measured in radians.
The Taylor series approximation works best for a small value of x.
For larger values, first compute x = x % (2 * pi).
>>> print(cos(Decimal('0.5')))
0.8775825618903727161162815826
>>> print(cos(0.5))
0.87758256189
>>> print(cos(0.5+0j))
(0.87758256189+0j)
"""
getcontext().prec += 2
i, lasts, s, fact, num, sign = 0, 0, 1, 1, 1, 1
while s != lasts:
lasts = s
i += 2
fact *= i * (i-1)
num *= x * x
sign *= -1
s += num / fact * sign
getcontext().prec -= 2
return +s
def sin(x):
"""Return the sine of x as measured in radians.
The Taylor series approximation works best for a small value of x.
For larger values, first compute x = x % (2 * pi).
>>> print(sin(Decimal('0.5')))
0.4794255386042030002732879352
>>> print(sin(0.5))
0.479425538604
>>> print(sin(0.5+0j))
(0.479425538604+0j)
"""
getcontext().prec += 2
i, lasts, s, fact, num, sign = 1, 0, x, 1, x, 1
while s != lasts:
lasts = s
i += 2
fact *= i * (i-1)
num *= x * x
sign *= -1
s += num / fact * sign
getcontext().prec -= 2
return +s
Decimal 常见问题
Q. 总是输入 decimal.Decimal('1234.5') 是否过于笨拙。在使用交互解释器时有没有最小化输入量的方式？A. 有些用户会将构造器简写为一个字母：
>>> D = decimal.Decimal
>>> D('1.23') + D('3.45')
Decimal('4.68')
Q. 在带有两个十进制位的定点数应用中，有些输入值具有许多位，需要被舍入。另一些数则不应具有多余位，需要验证有效性。这种情况应该用什么方法？A. 用 quantize() 方法舍入到固定数量的十进制位。如果设置了 Inexact 陷阱，它也适用于验证有效性：
TWOPLACES = Decimal(10) ** -2 # same as Decimal('0.01')
# Round to two places
>>> Decimal('3.214').quantize(TWOPLACES)
Decimal('3.21')
# Validate that a number does not exceed two places
>>> Decimal('3.21').quantize(TWOPLACES, context=Context(traps=[Inexact]))
Decimal('3.21')
Decimal('3.214').quantize(TWOPLACES, context=Context(traps=[Inexact]))
Traceback (most recent call last):
...
Inexact: None
Q. 当我使用两个有效位的输入时，我要如何在一个应用中保持有效位不变？A. 某些运算例如与整数相加、相减和相乘将会自动保留固定的小数位数。其他运算，例如相除和非整数相乘则将会改变小数位数，需要再加上 quantize() 处理步骤：
a = Decimal('102.72') # Initial fixed-point values
>>> b = Decimal('3.17')
>>> a + b # Addition preserves fixed-point
Decimal('105.89')
>>> a - b
Decimal('99.55')
>>> a * 42 # So does integer multiplication
Decimal('4314.24')
>>> (a * b).quantize(TWOPLACES) # Must quantize non-integer multiplication
Decimal('325.62')
>>> (b / a).quantize(TWOPLACES) # And quantize division
Decimal('0.03')
>>>在开发定点数应用时，更方便的做法是定义处理 quantize() 步骤的函数：
def mul(x, y, fp=TWOPLACES):
... return (x * y).quantize(fp)
>>> def div(x, y, fp=TWOPLACES):
... return (x / y).quantize(fp)
mul(a, b) # Automatically preserve fixed-point
Decimal('325.62')
>>> div(b, a)
Decimal('0.03')
>>>
Q. 表示同一个值有许多方式。数字 200, 200.000, 2E2 和 02E+4 的值都相同但有精度不同。是否有办法将它们转换为一个可识别的规范值？
A. normalize() 方法可将所有相同的值映射为统一表示形式：
values = map(Decimal, '200 200.000 2E2 .02E+4'.split())
>>> [v.normalize() for v in values]
[Decimal('2E+2'), Decimal('2E+2'), Decimal('2E+2'), Decimal('2E+2')]
>>>
Q. 有些精确数值总是被打印为指数表示形式。是否有办法得到一个非指数表示形式？A. 对于某些值来说，指数表示形式是表示系数中有效位的唯一办法。例如，将 5.0E+3 表示为 5000 可以让值保持恒定，但是无法显示原本的两位有效数字。如果一个应用不必关心追踪有效位，则可以很容易地移除指数和末尾的零，丢弃有效位但让值保持不变：
>>> def remove_exponent(d):
... return d.quantize(Decimal(1)) if d == d.to_integral() else d.normalize()
>>> remove_exponent(Decimal('5E+3'))
Decimal('5000')
Q. 是否有办法将一个普通浮点数转换为 Decimal？A. 有，任何二进制浮点数都可以精确地表示为 Decimal 值，但完全精确的转换可能需要比平常感觉更高的精度：>>>
>>> Decimal(math.pi)
Decimal('3.141592653589793115997963468544185161590576171875')
Q. 在一个复杂的计算中，我怎样才能保证不会得到由精度不足和舍入异常所导致的虚假结果。A. 使用 decimal 模块可以很容易地检测结果。最好的做法是使用更高的精度和不同的舍入模式重新进行计算。明显不同的结果表明存在精度不足、舍入模式问题、不符合条件的输入或是结果不稳定的算法。
Q. 我发现上下文精度的应用只针对运算结果而不针对输入。在混合使用不同精度的值时有什么需要注意的吗？A. 是的。原则上所有值都会被视为精确值，在这些值上进行的算术运算也是如此。只有结果会被舍入。对于输入来说其好处是“所输入即所得”。而其缺点则是如果你忘记了输入没有被舍入，结果看起来可能会很奇怪：
>>> getcontext().prec = 3
>>> Decimal('3.104') + Decimal('2.104')
Decimal('5.21')
>>> Decimal('3.104') + Decimal('0.000') + Decimal('2.104')
Decimal('5.20')
解决办法是提高精度或使用单目加法运算对输入执行强制舍入：
>>> getcontext().prec = 3
>>> +Decimal('1.23456789') # unary plus triggers rounding
Decimal('1.23')
此外，还可以使用 Context.create_decimal() 方法在创建输入时执行舍入：
>>> Context(prec=5, rounding=ROUND_DOWN).create_decimal('1.2345678')
Decimal('1.2345')
Q. CPython 实现对于巨大数字是否足够快速？
A. 是的。在CPython和PyPy3实现中，C/CFFI版本的decimal模块集成了高速libmpdec库，用于任意精度的正确舍入十进制浮点运算。
libmpdecc对中等数字使用Karatsuba乘法（ Karatsuba multiplication），对非常大的数字使用数论变换（Number Theoretic Transform）。
必须要对任意精度算术适配上下文。 Emin 和 Emax 应当总是设为最大值，clamp 应当总是设为 0 (默认值)。设置 prec 需要十分谨慎。
进行大数字算术的最便捷方式也是使用 prec 的最大值 ：
>>> setcontext(Context(prec=MAX_PREC, Emax=MAX_EMAX, Emin=MIN_EMIN))
>>> x = Decimal(2) ** 256
>>> x / 128
Decimal('904625697166532776746648320380374280103671755200316906558262375061821325312')
对于不精确的结果，在 64 位平台上 MAX_PREC 的值太大了，可用的内存将会不足:
>>> Decimal(1) / 3
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
MemoryError
在具有超量分配的系统上 (即 Linux)，一种更复杂的方式根据可用的 RAM 大小来调整 prec。假设你有 8GB 的 RAM 并期望同时有 10 个操作数，每个最多使用 500MB:
>>> import sys
>>>
>>> # Maximum number of digits for a single operand using 500MB in 8-byte words
>>> # with 19 digits per word (4-byte and 9 digits for the 32-bit build):
>>> maxdigits = 19 * ((500 * 1024**2) // 8)
>>>
>>> # Check that this works:
>>> c = Context(prec=maxdigits, Emax=MAX_EMAX, Emin=MIN_EMIN)
>>> c.traps[Inexact] = True
>>> setcontext(c)
>>>
>>> # Fill the available precision with nines:
>>> x = Decimal(0).logical_invert() * 9
>>> sys.getsizeof(x)
524288112
>>> x + 2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
decimal.Inexact: [<class 'decimal.Inexact'>]